Machine Learning: Regression | Machine Learning Specialization | Coursera

Brief Information

  • Name : Machine Learning:?Regression
  • Lecturer 😕Carlos Guestrin?and?Emily Fox
  • Duration: 2015-12-28 ~ 2016-02-15 (6 weeks)
  • Course : The 2nd(2/6) course of Machine Learning Specialization?in Coursera
  • Syllabus
  • Record
  • Certificate
  • Learning outcome
    • Describe the input and output of a regression model.
    • Compare and contrast bias and variance when modeling data.
    • Estimate model parameters using optimization algorithms.
    • Tune parameters with cross validation.
    • Analyze the performance of the model.
    • Describe the notion of sparsity and how LASSO leads to sparse solutions.
    • Deploy methods to select between models.
    • Exploit the model to form predictions.
    • Build a regression model to predict prices using a housing data set.
    • Implement these techniques in Python.

Syllabus ↑

Week 1 |?Simple Linear Regression
Welcome
  1. Welcome!
  2. What is the course about?
  3. Outlining the first half of the course
  4. Outlining the second half of the course
  5. Assumed background
Simple Linear Regression
  1. What is this course about?
  2. Regression fundamentals
  3. The simple linear regression model, its use, and interpretation
  4. An aside on optimization: one dimensional objectives
  5. An aside on optimization: multidimensional objectives
  6. Finding the least squares line
    1. Approach 1: Set gradient = 0
    2. Approach 2: Gradient descent
    3. Comparing the two approaches
  7. Discussion and summary of simple linear regression
    1. Influence of high leverage points
    2. High leverage points
    3. Influential observations
  8. Programming assignment
  1. Quiz: Simple Linear Regression
    1. Q&A
    2. interval, estimation, inverse estimation, unit change
  2. Quiz: Fitting a simple linear regression model on housing data
    1. A programming assignment
    2. 2 different models respectively by square feet and #bedrooms
Week 2 |?Multiple Regression
Multiple Regression
  1. Multiple features of one input
    1. Multiple regression intro
    2. Polynomial regression
    3. Modeling seasonality
    4. Where we see seasonality
    5. Where we see seasonality
    6. Regression with general features of 1 input
  2. Incorporating multiple inputs
    1. Motivating the use of multiple inputs
    2. Defining notation
    3. Regression with features of multiple inputs
    4. Interpreting the multiple regression fit
  3. Setting the stage for computing the least squares fit
    1. Optional reading: review of matrix algebra
    2. Rewriting the single observation model in vector notation
      1. Multiple regression by using matrices
    3. Rewriting the model for all observations in matrix notation
      1. Multiple regression by using matrices
    4. Computing the cost of a D-dimensional curve
      1. RSS of a D-dimensional curve
  4. Computing the least squares D-dimensional curve
    1. Computing the gradient of RSS
    2. Approach 1: closed-form solution
      1. Analogy by 1 dimension .
    3. Discussing the closed-form solution
      1. O(n^3): computationally intensive solution.
      2. There exist less intensive algorithms for the closed-form solution exist but the gradient descent is less intensive.
    4. Approach 2: gradient descent
      1. Just replace \nabla RSS(w^{(t)}) as -2 H^{T} (y - Hw )
    5. Feature-by-feature update
    6. Algorithmic summary of gradient descent approach
  5. Summarizing multiple regression
    1. A brief recap
    2. Quiz: Multiple Regression
  6. Programming assignment 1
    1. Reading: Exploring different multiple regression models for house price prediction
    2. Quiz: Exploring different multiple regression models for house price prediction
  7. Programming assignment 2
    1. Numpy tutorial
    2. Reading: Implementing gradient descent for multiple regression
    3. Quiz:?Implementing gradient descent for multiple regression
  1. Quiz: Multiple Regression
  2. Quiz: Exploring different multiple regression models for house price prediction
  3. Quiz: Implementing gradient descent for multiple regression
Week 3 |?Assessing Performance
Assessing Performance
  1. Defining how we assess performance
  2. 3 measures of loss and their trends with model complexity
  3. 3 sources of error and the bias-variance trade-off
    1. Irreducible error and bias
      1. 3 sources of error: Noise, bias, variance
      2. Noise is caused by neglected sources of the prediction.
      3. Noise: Irreducible error
      4. Bias(x) = f_{w(true)}(x) - f_{w(average)}(x)
      5. f_{w(average)}(x) = \frac{1}{N} \sum_{n=1}^{N} f_{w(trainingdata)}
      6. Low complexity ⇒ high bias
      7. High complexity ⇒ low bias
    2. Variance and bias-variance trade-off
      1. Low complexity ⇒ low variance
      2. High?complexity ⇒ high?variance
      3. Bias-variance trade-off
        1. Low complexity ⇒ high bias AND?low variance
        2. High?complexity ⇒ low bias AND high?variance
      4. Finding the sweet spot that complexity satisfies low bias and low variance
        1. MSE: Mean Squared Error
        2. MSE = \frac{1}{N} \sum_{n=1}^{N} \sqrt{Bias^2 + Variance}
      5. We cannot compute bias and variance because both contain the true function,?which cannot be computed.
    3. Error vs. amount of data
      1. For a fixed model complexity
      2. #(data points in training set) increases?⇒ training error increases
      3. #(data points in training set) increases?⇒ true error increases
      4. #(data points in training set) → ∞?⇒ [training error = true error]
  4. OPTIONAL ADVANCED MATERIAL: Formally defining and deriving the 3 sources of error
    1. Formally defining the 3 sources of error
    2. Formally deriving why the 3 sources of error
  5. Putting the pieces together
    1. Training/validation/test split for model selection, fitting, and assessment
      1. Hypothetical implementation
        1. Data set = (training set) + (test set)
      2. Practical implementation
        1. Data set = (training set) + (validation set) + (test set)
    2. A brief recap
    3. Quiz: Assessing Performance
  6. Programming assignment
    1. Reading: Exploring the bias-variance trade-off
    2. Quiz:?Exploring the bias-variance trade-off
  1. Quiz: Assessing Performance
  2. Quiz: Exploring the bias-variance trade-off
    1. Construction of polynomial regression using the linear regression function of graphlab.
    2. We can construct any polynomials using the linear combination by setting features as the powers of inputs.
    3. If the degree of the polynomial is too large.
    4. train_data : validation_data : test_data = 45 : 45 : 10
    5. The polynomial model is fitted on train_data.
    6. The RSS is computed on validation_data.
    7. Assessment is done on test_data.
    8. Choose the degree of the polynomial makes?the RSS(Residual Sum of Squares) on validation_data minimal among the candidate degrees.
Week 4 |?Ridge Regression
Ridge Regression
  1. Characteristics of over-fit models
    1. Symptoms of overfitting in polynomial regression
    2. Overfitting demo
    3. Overfitting for more general multiple regression models
  2. The ridge objective
    1. Balancing fit and magnitude of coefficients
      1. [measure of fit] ↘ ⇒ [good fit to training data]
      2. [measure of magnitude of coefficient]?↘ ⇒ [not overfit]
      3. [total cost] = [measure of fit] + [measure of magnitude of coefficient] = [RSS] + \sum_{j=0}^{D} \left \| \mathbf{w} \right \| _{j}^{2}
    2. The resulting ridge objective and its extreme solutions
      1. Select $latex \mathbf{\hat{w}}$??to minimize the total cost C_{total}
      2. $latex RSS(\mathbf{\hat{w}}) + \lambda \left \| \textbf{w} \right \|_{2}^{2}$
      3. \lambda = 0 \Rightarrow C_{total} = RSS(\mathbf{\hat{w}})
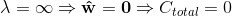
      4. CodeCogsEqn
        \lambda = \infty \Rightarrow \mathbf{\hat{w}} = 0?\Rightarrow C_{total} = 0
    3. How ridge regression balances bias and variance
      1. \lambda_{1} < \lambda_{2} \Rightarrow Variance_{1} < Variance_{2}
      2. \lambda_{1} < \lambda_{2} \Rightarrow Bias_{1} > Bias_{2}
    4. Ridge regression demo
      1. Underfit ↔ overfit
      2. “Leave One Out(LOO)” cross validation: the algorithm that chooses the tuning parameter, lambda \lambda
    5. The ridge coefficient path
      1. Coefficient path
  3. Optimizing the ridge objective
    1. Computing the gradient of the ridge objective
      1. <br /> RSS(\textbf{w}) + \lambda \left \| \textbf{w} \right \|_{2}^{2}<br />
      2. <br /> \left \| \textbf{w} \right \|_{2}^{2} = \textbf{w}^T \textbf{w}<br />
      3. <br /> \textbf{w} = (w_1\ w_2\ w_3\ ...\ w_D)^T<br />
      4. <br /> RSS(\textbf{w}) + \lambda \left \| \textbf{w} \right \|_{2}^{2}<br />
        <br /> = (\textbf{y}-\textbf{Hw})^{T}(\textbf{y}-\textbf{Hw}) +\lambda \textbf{w}^T \textbf{w}<br />
      5. <br /> \nabla [RSS(\textbf{w}) + \lambda \left \| \textbf{w} \right \|_{2}^{2}]\\<br />
        <br /> = \nabla [(\textbf{y}-\textbf{Hw})^{T}(\textbf{y}-\textbf{Hw})] +\lambda \nabla [\textbf{w}^T \textbf{w}]\\<br />
        <br /> = -2 \textbf{H}^T(\textbf{y}-\textbf{Hw}) + 2 \lambda \textbf{w}<br />
      6. COST
        <br /> \nabla cost( \textbf{w} )\\<br /> = -2 \textbf{H}^T(\textbf{y}-\textbf{Hw}) + 2 \lambda \textbf{w}\\<br /> =-2 \textbf{H}^T(\textbf{y}-\textbf{Hw}) + 2 \lambda \textbf{I} \textbf{w}<br />
      7. Ridge closed form solution
        <br /> \nabla cost( \textbf{w} ) = 0\\<br /> \Leftrightarrow \mathbf{H}^T \mathbf{H} \mathbf{\hat{w}} + \lambda \mathbf{I} \mathbf{\hat{w}} = \mathbf{H}^T \mathbf{y}\\<br /> \Leftrightarrow (\mathbf{H}^T \mathbf{H} + \lambda \mathbf{I})\mathbf{\hat{w}} = \mathbf{H}^T \mathbf{y}\\<br /> \Leftrightarrow \mathbf{\hat{w}} = (\mathbf{H}^T \mathbf{H} + \lambda \mathbf{I})^{-1} \mathbf{H}^T \mathbf{y}<br />
    2. Approach 1: closed-form solution
    3. Discussing the closed-form solution
    4. Approach 2: gradient descent
  4. Tying up the loose ends
    1. Selecting tuning parameters via cross validation
      1. How to choose the tuning parameter \lambda
      2. K-fold cross validation
      3. How to handle the intercept
      4. A brief recap
  5. Programming Assignment 1
  6. Programming Assignment 2
  1. Quiz: Ridge Regression
  2. Quiz: Observing effects of L2 penalty in polynomial regression
  3. Quiz: Implementing ridge regression via gradient descent
Week 5 |?Feature Selection & Lasso
Feature Selection & Lasso
  1. Feature selection via explicit model enumeration
  2. Feature selection implicitly via regularized regression
  3. Geometric intuition for sparsity of lasso solutions
  4. Setting the stage for solving the lasso
  5. Optimizing the lasso objective
  6. OPTIONAL ADVANCED MATERIAL: Deriving the lasso coordinate descent update
  7. Tying up loose ends
  8. Programming Assignment 1
  9. Programming Assignment 2
  1. Quiz: Feature Selection and Lasso
  2. Quiz: Using LASSO to select features
  3. Quiz: Implementing LASSO using coordinate descent
Week 6 |?Nearest Neighbors & Kernel Regression
Nearest Neighbors & Kernel Regression
  1. Motivating local fits
  2. Nearest neighbor regression
  3. k-Nearest neighbors and weighted k-nearest neighbors
  4. Kernel regression
  5. k-NN and kernel regression wrapup
  6. Programming Assignment
  7. What we’ve learned
  8. Summary and what’s ahead in the specialization
  1. Quiz: Nearest Neighbors & Kernel Regression
  2. Quiz: Predicting house prices using k-nearest neighbors regression
Closing Remarks

Summary

Glossary
  • Models
  • Fitted lines
  • Regression
  • Linear regression
  • Simple linear regression
  • Residual sum of squares [RSS]
  • The least square line
  • Gradient descent algorithm
    • Concave functions
    • Convex functions
    • Hill climbing
    • Hill descent
    • Step size
  • High leverage points
  • Influential observations
  • Multiple linear regression
  • Polynomial regression
  • Loss function
    • Squared error
    • Absolute error
  • Training data
  • Test data
  • Model complexity
  • fit ?a model to data
Sentences
  • The small mean of training errors doesn’t guarantee the small mean of test errors.
  • The smallest mean of training errors is not optimal for the mean of test errors.

 

  • adgads \nabla RSS(w^{(t)} ???asdfasd
  • ? $latex?\nabla RSS(w^{(t)} $

 

Related Posts

Leave a Reply

Your email address will not be published. Required fields are marked *