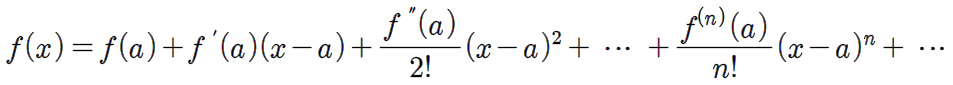Brief Information

• Name : Understanding Modern Mathematics 현대수학의이해
• Lecturer : 허민?Min Her
• Semester : 2016 Fall
• Major?: BS, Mathematics
• Textbook
  • Howard Eves (2003) 『수학의 위대한 순간들』경문사
    • Korean translated version of the following two books. The two books is merged into this Korean edition.
    • Howard Eves (1980)?Great Moments in Mathematics Before?1650. Mathematical Assn of Amer
    • Howard Eves (1983) Great Moments in Mathematics After 1650.?Mathematical Assn of Amer
• Syllabus : Syllabus_2016-5-2__Understanding Modern Mathematics.pdf
• In?short
  • This course deals with the Great Moments in Mathematics Since 1635.
• Test
  • Definitions, algorithms, or methods are on the midterm exam. Be aware of the definitions and how to solve the problems in the lectures.

---

Summary

The starting number is 18.

18) 17세기 수학

• 17세기는 수학을 완전히 새로운 기초 위에 세웠다.
• 르네 데카르트, 뉴턴, 라이프니츠, 페르마, 파스칼
• 17세기 후반기에 이르러, 미분 적분학이 출현할 수 있는 원자료들이 가까이에 널려 있었다. 남은 것은 라이프니츠나 뉴턴이 그런 발상들을 유합시켜서 엄청난 통합으로 이끌어내는 일만 남아 있었다.
• 토리첼리(Evangelista Torricelli, 1608~1647)
  • 한 없이 길지만 부피가 유한인 기하학적 입체 ‘뾰족한 쌍곡선 입체(acute hyperbolic solid)’가 존재한다는 사실 입증.
• 마랭 메르센(Marin Mersenne, 1588~1648)
  • 과학자들의 발상을 교환하기 위한 어느 정도 정기적인 학술 모임(conference)을 유지(1635~1648).
• 연구 기관
  • 런던 왕립 학회
  • 프랑스 왕립 과학원
  • 베를린 왕립 과학원
  • 상트페테르부르크 과학원

19) 카발리에리의 불가분량의 방법(1635년)

카발리에리의 원리(Cavalieri’s Principle)

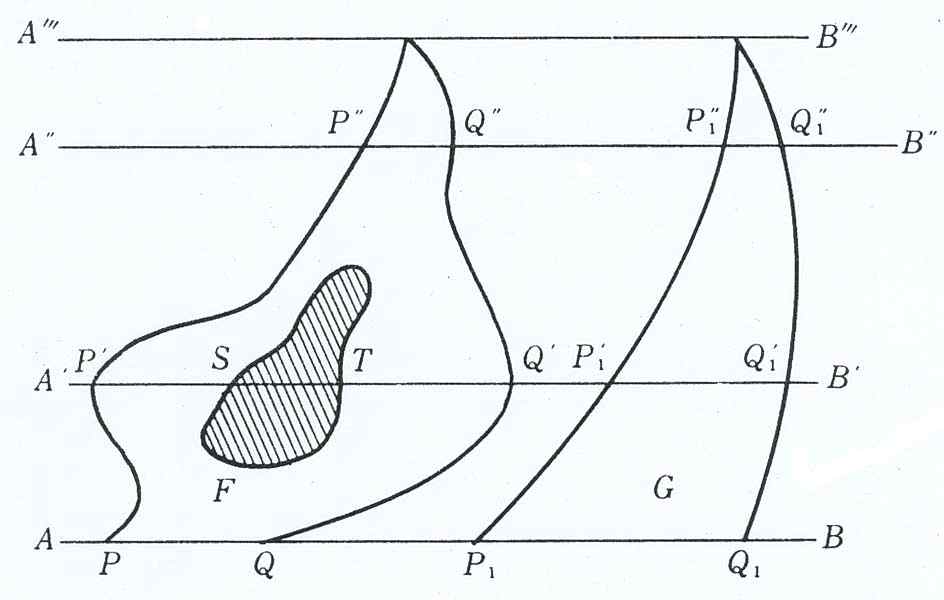
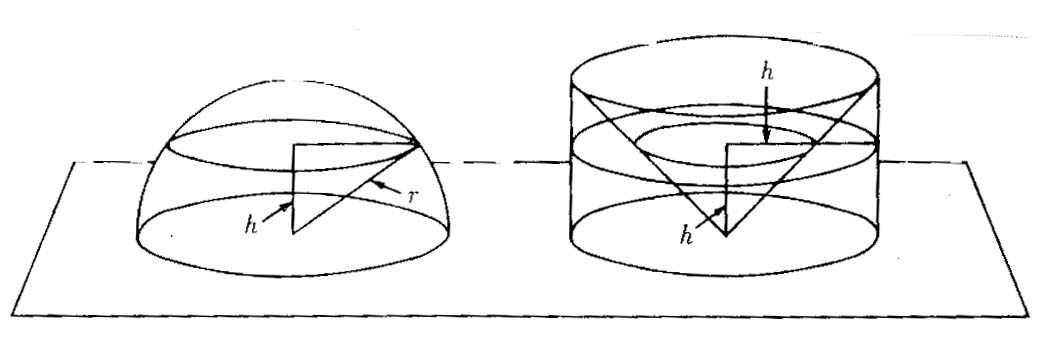
1. 평면도형에 대한 카발리에리의 원리
   • 두 개의 평면 도형이 한 쌍의 평행선 사이에 끼어 있고 그 평행선들과 평행인 임의의 선(불가분량:= 선분)으로 그 두 평면 도형을 잘랐을 때 생기는 두 선분의 길이 사이의 비가 항상 일정하면, 두 평면 도형의 넓이 사이의 비도 또한 그와 같다.
     
     
2. 입체도형에 대한 카발리에리의 원리
   • 두 개의 입체 도형이 한 쌍의 평행면 사이에 끼어 있고 그 평행면들과 평행인 임의의 면으로 그 두 입체 도형을 잘랐을 때 생기는 두 단면(불가분량:= 단면)의 넓이 사이의 비가 항상 일정하면, 두 입체 도형의 부피 사이의 비도 또한 그와 같다.
     

기타

• 불가분량의 방법에는 엄밀한 기초가 없다.
• 틀린 답을 얻기도 한다. 호이겐스가 밝혔다.
• 의문
  • 1차원 선분들이 모이면 2차원 단면이 되는가.
  • 2차원 단면들이 모이면 3차원 입체가 되는가.
  • 현대 기하에서 점, 선, 면은 무정의 용어(primitive notion)다.

20)?해석 기하학의 발견(1637년)

• 해석 기하학 (analytic geometry)
  • 기하학의 한 분야가 아니라 한 방법이다.
  • 기하학 문제 → (변환)?→ 대수학 문제?→ (풀이)?→ (역전)?→ 기하학 문제 해결
  • 도형만으로 알 수 없는 미세한 문제도 발견할 수 있다.
• 해석 기하학 적용 예
  • 내외분점 공식
  • 원뿔 곡선(=이차 곡선): 원(circle), 타원(ellipse), 포물선(parabola), 쌍곡선(hyperbola)
    • 원의 방정식을 구하기(중심)
    • 타원의 방정식을 구하기(두 초점)
    • 포물선의 방정식을 구하기(초점과 준선)
    • 쌍곡선의 방정식을 구하기(두 초점)
    • 컴퓨터 화면이 좌표 평면. 기하를 해석 기하학으로 표현.
• 종합 기하학과 해석 기하학
  • 종합적인 방법에서는 ‘경험과 시행착오에 의존‘해 문제를 해결하지만, 해석적방법에서는 ‘통상 따라가야하는 뚜렷한 단계(알고리즘)‘에 따라 문제를 해결한다.
  • 해석적인 방법이 종합적인 방법보다 적용 범위가 넓고 적용하기가 더 쉽다.
• 해석 기하학의 발견자, 르네 데카르트(Rene Descartes, 1596~1650) (+페르마)
  • 자연철학에 대한 책. 《우주론》,?《철학의 원리》. 태양 중심설.
  • 1637년, 학문에서 진리를 찾기 위해 이성을 올바르게 이끄는 방법 서설.
  • 1649년, 스우덴 여왕 크리스티나(1626~1689)의 초청으로 스톡홀름으로 이주.
  • 1650년 2월 1일에 감기에 걸려 사망.
• 《방법서설》
  • 프랑스 말로 저술.
  • 공식적인 철학 전문 서적이 아니라 데카르트가 자신의 방법에 도달한 과정에 대한 자서전식의 간략한 개요.
  • 세 가지 부록(굴절 광학, 기상학, 기하학)은 과학적 진리를 찾는 데카르트의 새로운 방법을 구체적으로 보여주는 실례였고, 방법 서설은 이에 대한 머릿말로 의도되었다.
• 《기하학》
  • 제1부: 대수적 기하학
  • 거듭제곱에 대한 현대적인 표기를 사용.
  • 현대적인 직교 좌표 체계가 전혀 나타나지 않는다. 그러나 사교 좌표 체계를 선택했다. x와 y의 양수 값만을 사용, 즉 제1사분면으로 제한했다. 좌표(coordinate)라는 용어는 이 책에 나타나지 않는다.
  • 데카르트의 부호 법칙(Descartes’s rule of signs)
    • 계수가 실수이고 $latex a_n > 0$인 방정식 $latex f(x)=a_0 x^n + a_1 x^{n-1} + … +a_{n-1} x + a_{n}$?의 양수 근의 개수는 (각 근을 중복된 횟수만큼 세면) 계수에서 부호 변동의 개수와 같거나 이 개수보다 양의 짝수만큼 작은 수이다.
    • 음수 근의 개수를 추정할 때는 $latex x$에?$latex (-x)$를 대입하면 된다.
• 피에르 드 페르마(Pierre de Fermat, 1601?~1665)
  • 아포로니오스의 <평면의 자취>
  • 직선, 원, 쌍곡선, 타원, 포물선 등의 방정식을 논의
  • 접선과 구적에 관한 논문
  • 직교 좌표계도 이용. 제1사분면만 이용.
  • 데카르트보다 많은 새로운 곡선을 제시했다.
  • [연구의 방향] 데카르트: 궤적 → 궤적의 방정식, 페르마: 방정식 → 방정식의 궤적

21)?수학적 확률론의 탄생(1654년)

• 통계적 확률, 수학적 확률
• 주사위, 카드 놀이.
• 카르다노 《우연의 놀이에 관한 책》
• 파스칼과 페르마의 서신 왕래를 통한 확률 문제 추론의 사슬이 오늘날 우리가 알고 있는 확률 이론을 제공했다.
• 메레가 파스칼에게 문의, 파스칼의 확률론 연구, 페르마와 서신 왕래
• 득점의 문제(problem of the points)
  • 똑같은 정도의 능력을 지닌 두 경기자 사이에서 경기가 중단되었을 경우 판돈을 분배할 것인가?
  • 예: 두 경기자 A와 B에 대해서 A가 승리하기 위해서는 2득점이 더 필요하고 B가 승리하기 위해서는 3득점이 필요한 경기에서 판돈을 분배하는 방법을 찾아라.
  • 페르마의 해결방법: 순열
  • 파스칼의 해결방법: 파스칼의 삼각형
• 블레즈 파스칼(Blaise Pascal, 1623~1662)
  • 신비로운 육각형 정리: “원뿔 곡선에 내접하는 육각형의 세 쌍의 대변의 세 교점은 한 직선 위에 있다.”
    
  • 덧셈 기계 Pascaline 발명
  • 《산술 삼각형 개론》에서 산술 삼각형(파스칼의 삼각형)의 19가지 성질을 소개.
  • 수학적 귀납법(드 모르간이 명명)에 대한 명확한 공식화를 《산술 삼각형 개론》에서 소개.
  • 굴렁쇠선(cycloid)에 대한 연구.
  • 파스칼의 삼각형: 이항계수 얻기. 동양에서 먼저 기록됨.
• 확률의 정의
  • 수학적 확률
  • 통계적 확률
  • (possibility, probability)
• 사건, 시행, 근원사건
• 확률론에 기여한 사람들
  • 크리스티안 하위헌스(호이겐스, Christiaan Huygens, 1629~1695)
    • 확률에 대한 최초의 공식적인 논문 ‘우연의 놀이에서의 추론에 대해(De Ratiociniis in Ludo Aleae)’
    • 기댓값 개념 제시.
  • 야코프 베르누이(Jabcob Bernoulli, 1654~1705)
    • 베르누이 분포, 베르누이 정리.
    • 확률론에 대한 최초의 책 ‘추측술(Ars conjectandi)’
  • 아브라함 드무아브르(Abraham De Moivre, 1667~1754)
    • 책 발간 ‘우연의 원리, 놀이에서 사건의 확률을 셈하는 방법(1718)’
    • n의 계승(factorial)의 근사식을 구하는 식 제시
  • 다니엘 베르누이(Daniel Bernoulli, 1700~1782)
    • ‘상트페테르부르크(Saint Petersburg) 문제 또는 역설’에 대한 고찰 결과를 상트페테르부르크 과학원의 ‘회보’에 발표. 무한대로 던지기를 시행할 때 기댓값은 무한대.
  • 피에르 시몽 라플라스(Pierre Simon Laplace, 1749~1827)
    • 책 ‘확률의 해석적 이론(1812)’ 발간. (*메모: 측도론 measure theory. Probability is one of measures. 확률론을 하기 위해서는 해석학, 측도론을 알아야한다.)
  • 시메옹 드니 푸아송(Poisson)
• 상트페테르부르크 수학 학파
  • 파프누티 체비쇼프(Pafnuty Chebyshev, 1821~1894)
  • 안드레이 마르코프(Andrei Markov, 1856~1922)
  • 안드렝이 콜모고르프(Andrei Kolmogorov, 1903~1987)
    • 1920년대 후반 확률 이론이 대한 공리 체계 전개. 3개의 공리.
      • $latex 0<=P(B)<=1$
      • $latex P(\Omega)=1$
      • $latex P(B_1 \cup B_2)=P(B_1)+P(B_2)$

22)?미분학의 발견(1629년-1680년대)

• 뉴턴과 라이프니츠에 의해 17세기 말에 미분학이 시작되었다.
• 이전에는 수학은 기하학과 대수학의 정적인 대상에 대한 학문이었다. 미분학에 의해 동적인 대상(운동)을 수학은 포함하게 되었다.
• 접선 작도법: 곡선은 한 점에 의해 생성되고, 생성 점의 운동은 두운동의 합성이며, 두 운동의 속도 벡터의 합성은 곡선의 접선이 된다. 예: 포물선. (질 페르손 드 로베르발 Gilles Persone de Roberval, 1602~1675) 이 방법은 모든 도현에 일반적으로 적용할 수 없다.
  
• 최댓값·최솟값을 찾는 ‘페르마의 방법‘
  • 페르마의 방법
    1. 매우 작은 $latex e$에 대해?$latex f(x+e)\approx f(x)$이다.
    2. $latex f(x+e)=f(x)$를 풀고 $latex e=0$을 대입한다.
    3. 방정식의 근에서?$latex f(x)$는?최댓값 또는 최솟값을 가진다.
  • 페르마의 방법의 예제
    
  • 페르마의 발상은 $latex f'(x)=\lim_{h\to 0} \frac{f(x+h)-f(x)}{h} =0$ 과 동치이다.
  • $latex f'(x)=0$ 이 되는 것은 최댓값·최솟값이 되기 위한 필요충분조건이 아닌 피요조건이라는 사실을 페르마는 깨닫지 못했다.
• 페르마의 ‘곡선의 접선을 찾는 방법‘
  • 곡선의 접선을 찾는 방법
    1. 곡선 $latex f(x,y)=0$의 점 $latex (x,y)$에 대한 이 곡선의 접선영 $latex t$를 찾자.
    2. 닮은꼴 삼각형을 이용하면, 접점과 가까운 접선에 있는 점의 좌표는 다음과 같다. $latex (x+e, y(1+e/t))$
    3. 이 점을 곡선에 있는 점으로 간주하자.?$latex f(x+e, y(1+e/t))=0$
    4. $latex e=0$을 대입해서 접점의 좌표 $latex x$와 $latex y$의 항으로 접선영 $latex t$를 구한다. 이것은 다음과 동치이다. $latex t=-y\frac{\partial f/\partial y}{\partial f/\partial x}$
• 배로의 ‘곡선의 접선을 찾는 방법‘
  • 곡선의 접선을 찾는 방법
  • 예제
• 도함수 계산을 위한 체계적인 해석학적 방법과 일반적인 기호의 발견, 즉 적합하고 실행 가능한 미분법의 발견 -?뉴턴, 라이프니츠
• 미분법의 기초에 대한 모순되지 않고 엄밀한 전개 – 코시(1789~1857)와 19세기의 후계자
• 라이프니츠(Gottfried Wilhelm Leibniz)의 미분학
  • 예제
  • 무한소(infinitesmal)의 개념 이용. 개념: ‘0이 아니라서 나눗셈의 몫이 될 수 있지만 나중에 0으로 생각해도 좋다.’
• 뉴턴(Isaac Newton)의 유율법
  • 물리적인 접근 방법
  • ‘곡선은 한 점의 연속적인 운동으로 생성’
  • 유량(fluent): $latex x,y,\dot y$
  • 유율(fluxion):?$latex \dot x,\dot y,\ddot y$
  • 유량 x의 모텐트 $latex \dot x o$
  • $latex x=x(t), \dot x =f'(x), \dot x o=f'(x)dt$
  • 예제
    
  • 뉴턴이 고려한 두 가지 형태의 문제
    • 유량들의 관계로부터 유량들과 그것들의 유율들 사이의 관계 찾기 – 미분법
    • 유량들과 그것들의 유율들 사이의 관계로부터, 유량들만의 관계를 찾기 – 미분 방정식의 풀이

미분학 발견자들과 그 우선권 논쟁

• 아이작 뉴턴 (Isaac Newton, 1642~1727)
• 고트프리트 라이프니츠?(Gottfried Wilhelm Leibniz, 1646~1716)
• 뉴턴이 라이프니츠보다 먼저 미적분을 발견.
• 뉴턴이 라이프니츠에게 자신의 미적분 발견 결과를 암시하기 위해 서신을 보냈다.
• 여러 서신 중에 미적분 발견 결과를 미적분 발견 결과를 암시하기 위한 서신을 보내고 그 결과는 암호화해서 보냈다. 그 편지는 라이프니츠가 미적분을 발견하고 나서 보았다.
• 뉴턴은 라이프니츠의 미적분에 대한 독립적인 발견을 인정했다.
• 나중에 뉴턴과 라이프니츠 이외 저술가들이 두 학자의 결과 중 하나가 배낀 것이라는 말을 하므로서 잉글랜드와 유럽 대륙의 수학 교류가 약해졌다. 결국, 잉글랜드 학자들은 라이프니츠의 미적분학의 장점을 받아드리지 못해서 미적분학을 해석적으로 발전시키지 못했다.
• 뉴턴의 미적분: 기하학적, $latex \dot x$ 표기법
• 라이프니츠의 미적분: 해석적, $latex \frac{dx}{dt}$ 표기법

23)?미분적분학의 기본 정리(1669년-1690년대)

로베르발

• 1634년 굴렁쇠선의 한 아치 아래 넓이는 생성원 넓이의 3배이다.

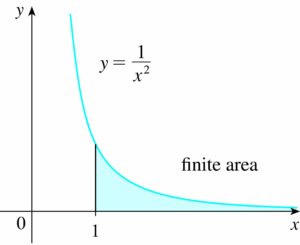
토리첼리

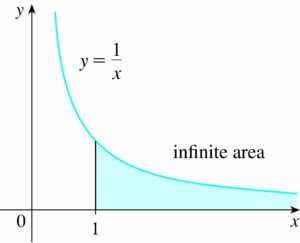
• $latex \int_{1}^{\infty}\frac{1}{x}dx=[lnx]_{1}^{\infty}=\infty$
• $latex \int_{1}^{\infty}\frac{\pi}{x^2}dx=[-\frac{\pi}{x}]_1^\infty=\pi$
• 임을 발견.

• 함수 $latex y=x^n$에 관하여 미분 적분 연산의 관계를 인식.

뉴턴과 라이프니츠

• 대수학적인 접근으로 / 적분을 형식적으로 수행할 수 있는 도구로서 / 미적분학
  의 기본 정리를 활용

미적분학의 기본정리

정 적분의 기본 정리

?

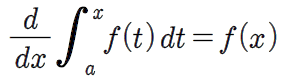
적분과 미분의 관계

24) 거듭제곱 급수, 테일러 급수와 매클로린 급수(1715년, 1742년)

수열(sequence)과 급수(series)

• 수열
• 급수

x-a에 관한 거듭제곱 급수

x에 관한 거듭제곱 급수

테일러 급수

매클로린 급수

테일러 급수와 매클로린 급수의 용도

• 삼각 함수, 로그 함수, 지수 함수값의 근사값을 구하는데 쓰인다.
  • 예를 들어, 테일러 급수나 매클로린 급수의 5째 항까지 구하고 그 값을 근사값으로 쓴다.

 

특강) 산학수열

• 묵사집산법
• 구장산술 – 유희
• 쇠분[=분배] 문제
• 산학계몽 – 주세걸
  • 고려 시대에 전해짐. 산사를 뽑는데 사용된 교과서.

?묵사집산법

• 등차 수열
  • <제1문>
    지금 갑, 을, 병 세 사람이 함께 나누어 가질 쌀이 38섬 7말 있다. 다만, 갑은 4분을 취하고 을은 3분을 취하며 병은 2분을 취한다고 한다. 각자의 몫은 얼마인가?
  • <제25문>
    지금 대의 마디가 7개 있는데, 아래 2마디에는 쌀이 3되 담기고 위 3마디에는 쌀이 2되 담긴다. 가운데 2마디 및 각 마디에 담기는 쌀은 얼마인가?
  • <제27문>
    지금 대의 마디가 9개 있는데, 아래 2마디에는 쌀이 3되 담기고 위 3마디에는 쌀이 2되 담긴다. 가운데 4마디 및 각 마디에 담기는 쌀은 얼마인가?
• 등차 수열의 응용
  • <제15문>
    지금 9등급으로 나뉘어 세금을 내는 가구들이 있는데, 갑등은 364호, 을등은 396호, 병등은 432호, 정등은 570호, 무등은 584호, 기등은 676호, 경등은 850호, 신등은 920호, 임등은 1608호이고, 세금으로 거둔 전체 식량은 65664섬이다. 다만, 갑부터 임까지 각 등 1호의 차수는 1섬 6말이다. 매호가 내는 세금 및 각 등급 전체 가구가 내는 합은 얼마인가?
• 등비 수열
  • <제16문>
    지금 사람이 돈 1문을 가지고 있는데, 첫날부터 하루에 1배씩 증가하여 30일까지 매일 배가 된다. 전체의 돈은 얼마인가? (등비 수열의 30번째 항)
  • <제17문>
    지금 사람이 있는데, 첫날에 돈 3문을 만들고 이후 날마다 차례로 3배하여 한 달 동안 계속한다. 전체의 돈은 얼마인가? (등비 수열의 28/29/30/31번째까지 항의 합)
• 등비 수열의 합
  • <제6문>
    지금 갑, 을, 병, 정 네 사람이 함께 나누어 가질 실이 115근 13양 4전 있다. 다만, 위로부터 절반 차로 이를 나눈다. 각자의 몫은 얼마인가?
  • <제1문>
    지금 술을 가지고 봄 놀이를 가는 사람이 있는데, 그 술의 양은 알지 못한다. 다만, 술집을 만나 1배를 사서 더하고 꽃을 만나 3말 6되를 마셨다. 또, 남은 술을 가지고 또 1배를 사고 또 3말 6되를 마셨다. 만약 이와 같이 5차례 하면 술이 다하고 술병이 빈다. 원래 가져 간 술은 얼마인가?
  • <제3문>
    지금 뜰에서 함께 난 소나무와 대나무가 있는데, 첫째 날 소나무는 6자 자라고 대나무는 7치 반 자란다. 다만, 첫날 이후 소나무는 날마다 전 날 자란 것의 반만큼 자라고 대나무는 날마다 전 날 자란 것의 갑절만큼 자란다고 한다. 소나무와 대나무는 몇째 날 길이가 같아지는가?
  • <제7문>
    지금 갑, 을, 병, 정 네 사람이 함께 나누어 가질 실이 544근 있다. 위로부터 46(사륙) 차로 이를 나눈다. ?주: 위로부터 10분을 비율로 삼아 차례로 4분을 빼고 6분을 취하는 것과 같음을 이른다.? 각자의 몫은 얼마인가?
  • <제8문>
    지금 갑, 을, 병, 정 네 사람이 함께 나누어 가질 돈이 1276관 있다. 다만, 을은 갑의 7분의 3과 같고 병도 역시 을의 7분의 3과 같으며 정도 역시 병의 7분의 3과 같아서, 모두 37(삼칠) 차로 차례로 이를 나눈다고 한다. 각자의 몫은 얼마인가?
  • <제14문>
    지금 갑, 을, 병, 정, 무, 기 6국이 함께 나누어 가질 실이 4860근 있다. 서양 비단을 짜는데, 6국으로 하여금 위로부터 28(이팔) 차로 이를 나눈다. 그 비단 한 필에 들어가는 실은 2근 4양이고, 한 필의 길이는 3장 2자이다. 나누어 가질 실과 짜야 할 비단은 각각 얼마인가?
• 등비 수열의 응용
  • 세금 또는 분배와 관련된 문제로, 묵사 인 차등균배문의 제10, 11, 12, 16문은 등비 수열을 응용하고 있다.
• 항 사이의 비가 바뀌는 수열
  • <제9문>
    지금 갑, 을, 병, 정, 무 다섯 사람이 함께 나누어 가질 은이 447양 있다. 다만, 을(의 은)은 갑(의 은)의 9분의 7과 같고, 병은 을의 7분의 5와 같고, 정은 병의 5분의 3과 같고 무는 갑의 51분의 13과 같다고 한다. 각자의 몫은 얼마인가?
• 쌓기 문제
  • <제1문> (2차원 쌓기 문제)
    지금 평첨초가 한 더미 있는데, 각 면의 아랫줄에 52퇴 있다. 모두 몇 퇴인가?
  • <제7문> (3차원 쌓기 문제)
    지금 삼각과가 한 타 있는데, 각 면의 아랫줄에 28개씩 있다. 모두 몇 개인가?
  • <제18문>
    지금 삼각과일타가 있는데, 모두 8436개이다. 각 면의 아랫줄에는 몇 개 있는가?
• 천원술
  • 천: x, 원: 미지수, 술: 방법
  • 방정식을 푸는 방법
• 증승개방법에 의한 풀이(★시험)
  • ‘루피니-호너의 방법’과 동일
  • 계수가 큰 방정식을 증승개방법으로 푸는 문제 출제
• 수열의 합
  • <제2문>
    지금 원전이 한 묶음 있는데, 바깥 둘레에 84(=n)척 있다. 모두 몇 척인가?
  • <제3문>
    지금 방전이 한 묶음 있는데, 바깥 둘레에 68(=n)척 있다. 모두 몇 척인가?
  • <제4문>
    지금 세모꼴 산대가 한 묶음 있는데, 바깥 둘레에 90(=n)척 있다. 모두 몇 척인가?
  • <제6문>
    지금 부병이 한 타 있는데, 너비를 따라 9개 있고 길이를 따라 14개 있다. 모두 몇 개인가?
  • <제8문>
    지금 사각과가 한 타 있는데, 각 면의 아랫줄에 28개씩 있다. 모두 몇 개인가?
• 이선란(李善蘭, 1811~1882)
• 급수에 대한 조선 산학자 이상혁(李尙爀, 1810~?)

25)?푸리에 급수(1807년)

18세기의 수학과 수학자

• 18세기는 미분 방정식의 세기

야코프 베르누이(Jacob Bernoulli, 1654~1705)

요한 베르누이(Johann Bernoulli, 1667~1748)

• 야코프 베르누이의 아들
• 라이프니츠의 1684년 미분학, 1686년 적분학 논문 연구. (라이프니츠 → 야코프 베르누이 →?요한 베르누이 → 로피탈 → 하이헌스)

다니엘 베르누이(Daniel Bernoulli, 1700~1782)

• 유체 역학에서 베르누이의 법칙(Bernoulli’s Principle)을 발견

레온하르트 오일러(Leonhard Euler, 1707~1783)

• 요한 베르누이의 제자
• 다니엘 베르누이의 친구
• 스위스?→ 러시아?→ 프로이센(독일)?→ 러시아
• 수학 저체 역사에서 가장 많은 글을 남겼다.
• $latex \sum_{n=1}^{\infty } \frac{1}{n^2}=\frac{\pi^2}{6}$
• $latex \sum_{n=1}^{\infty } \frac{1}{n^{2k}} (k\in\mathbb{N})$ 일반화
• 해석학에 관한 중요한 3개의 책 발간: 《무한 해석 입문》,?《미분학 원리》,?《적분학 원리》
• 쾨니스베르그 다리 문제에 대한 논문 출판. 그래프 이론(graph theory)의 시작.
• $latex 2^{2^{5}}+1$가 소수(prime)가 아님을 밝혔다. 즉,?$latex 2^{2^{n}}+1 \ (n \in \mathbb{N})$ 가 항상 소수가 아님을 밝혔다.

알렉시스클로드 클레로(Alexis-Claude Clairaut, 1713~1765)

장르롱 달랑베르(Jean-le-Rond d’Alembert, 1717~1783)

요한 람베르트(Johann Heinrich Lambert, 1728~1777)

조제프 루이 라그랑주(Joseph Louis Lagrange, 1736~1813)

• 해석학의 기초를 다짐.
• 오일러에 대적할 만한 학문적 업적을 남겼다. 논문 양은 오일러보다 작지만 질이 우수했다.
• 라그랑주의 정리(Lagrange theorem)
• 변분법(calculus variation)을 창시
• 《해석 역학》저술

콩도르세(M-J. A-N, C. Condorcet, 1743~1794)

가스파르 몽주(Gaspard Monge, 1746~1818)

• 《화법 기하학》저술

피에르 시몽 라플라스(Pierre-Simon Laplace, 1749~1827)

• $latex \int_{-\infty }^{\infty } e^{-x^2}dx=\sqrt{\pi}$을 증명했다.
• Laplace transform: $latex f(x)=\int e^{-xt}g(t)dt$
• Vector Laplacian operator: $latex \bigtriangledown ^2u=u_{xx}+u_{yy}+u_{zz}$
• The Laplace equation:?$latex u_{xx}+u_{yy}+u_{zz}=0$

아드리앵마리 르장드르(Adrien-Marie Legendre, 1752~1833)

• 이차 상호 법칙, 소수 법칙, 최소 제곱 방법 발견.
• 훌륭한 발견에도 불구하고 가우스가 자신의 업적이라고 주장하는 등 다툼이 있었다.

라자르 카르노(Lazare Carnot, 1753~1823)

• 위치 기하학

푸리에 급수 Fourier Series

장 바티스트 조제프 푸리에?(Jean-Baptiste-Joseph Fourier, 1768~1830)

푸리에 급수 Fourier Series

• “갇히고(bounded) 닫힌(closed) 구간에서 정의된 모든 함수를 완전히 사인 함수들과 코사인 함수들의 합으로 표현할 수 있다.”
• 곧, 구간 에서 정의된 임의의 함수 는 다음과 같은 푸리에 급수 와 같다.
  • $latex S(x)=a_0 / 2 + \sum_{n=1}^{\infty}(a_n cos(nx) + b_n sin(nx))$
  • a_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)cos(nx)dx
  • b_n=\frac{1}{\pi}\int_{-\pi}^{\pi}f(x)sin(nx)dx
• 푸리에 급수는 많은 연구 주제를 만들어 냈다.
• 테일러 급수는 무한히 미분가능한 함수를 무한 급수로 표현할 수 있다.
• 푸리에 급수는 일계 적분이 가능하다면 무한 급수로 표현할 수 있다. 테일러 급수보다 적용 범위가 넓다.
• FFT: Fast Fourier Transformation. A great approximation method.

디리클레(Peter Gustav Lejeune Dirichlet, 1805~1859)의 정리

• “함수$latex f(x)$는 닫힌 구간 $latex [-\pi, \pi]$에서 갇혀 있고 유한개의 불연속점과 유한개의 극댓값과 극솟값이 존재하면, $latex f(x)$의 푸리에 급수는 $latex f(x)$가 연속인 모든 점에서 $latex f(x)$에 수렴하고 $latex f(x)$가 불연속인 각 점에서는 $latex f(x)$의 왼쪽 극한 값과 오른쪽 극한 값의 평균값에 수렴한다.”
• 이 정리를 이용하면 거의 모든 함수를 푸리에 급수로 표현할 수 있다.
• “함수를 푸리에 급수로 나타내어라” (★이번 중간고사에 출제)

페터 구스타프 레조이네 디리클레?(Peter Gustav Lejeune Dirichlet, 1805~1859)

• 1837년 디리클레의 정리 증명 “$latex gcd(a,b)=1$인 옹근 수들의 임의의 등차 수열 $latex a, a+d, a+2d, …$ 에는 씨수(prime)가 무수히 많이 포함되어 있다.”

---

기말고사 범위는 여기부터 끝까지.

26)?비유클리드 기하학의 발견(1829년)

19세기와 20세기의 수학

19세기

• 19세기 이후, 수학 논문이 급격하게 많아졌다.
• 대학이 발달하면서 전문 수학자들이 대거 등장했다.
• 도이칠란드가 우세
• 비유클리드 기하학의 발견 (1829년)
• 비가환 대수학의 발견 (1843년)
• 해석학의 산술화 (19세기 말)
• 집합론 등장. 수학 전만에 걸친 일반화와 추상화 (19세기 말)

20세기

• 미국 대학이 우세
• 20세기부터 미국에서 박사 학위 수여 건수가 도이칠란드를 능가하기 시작함.
• 수학의 기초에 대한 논쟁이 일어났고 논리주의, 직관주의, 형식주의가 등장함.
• 수학의 각 분야의 공리화.

비유클리드 기하학의 발견 1

평행선 공준 parallel postulate

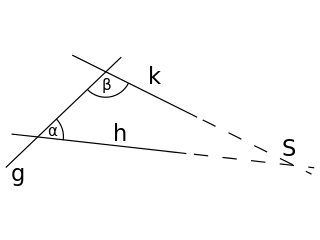
• 정의: 한 직선 g가 두 직선 h와 k와 만나고, 같은 쪽에 있는 두 내각 의 합 $latex \alpha + \beta$가 평각보다 작으면, 그 두 내각과 같은 쪽에서 두 직선 h와 k가 한 점 S에서 만난다.

• 평행선 공준은 공준이기에는 간단하지 않고 자명하지 않다. 그래서 이 공준을 더 간단한 명제로 만들기 위해 이 공준과 동치인 명제를 찾는 시도가 많았다. 다른 방면으로, 평행선 공준이 복잡해 보여서 공준이 아닐 수 있다는 느낌을 주었기 때문에 동치인 명제를 찾으려 노력했다.
  • =평행선 공준은 다른 공리(公理)와 공준(公準)과 달리 복잡하고, 질적으로 다르다고 생각되어, 이것을 부정하는 기하학 이론체계가 시도되었다.
• ” 평행선 공리는 다른 공리들에 대해 독립적이며 다른 공리들로부터 유도되지도 않는다. 다른 공리로 부터 평행선 공리를 유도하려는 수 많은 시도가 있었으나 모두 실패하였고, 근대에 이르기까지 미해결 문제로 남아있었다.” – 기하학사 | 위키 백과
• 가우스의 비유클리드 기하학 발견
  • “삼각형의 세 내각의 합이 180도보다 작다고 가정하니까 우리가 지금까지 알고 있는 기하학과는 전혀 다른 이상한 기하학이 생겼는데, 아무리 살펴 보아도 모순이라고는 전혀 찾아볼 수가 없어서 나는 아주 만족스럽네. …… 내 발견을 논문으로 발표하는 일은 내 생전에는 있지 않을 거야. 왜냐하면 내가 이것을 발표하면 아둔한 사람들이 얼마나 악을 쓰면서 덤비겠어. 그게 겁나네.”- 기하학사 | 위키 백과

비유클리드 기하학의 발견 2

• 비유클리드 기하학의 정의
  • 유클리드 공간이 아닌 공간에서 다루는 모든 기하학을 총체적으로 가리키는 말.
  • 유클리드 기하학의 제5공준(公準)-평행선 공준-의 부정 공리를 취한 기하학 이론체계이다.
  • 비유클리드 기하학에서는 평행선 공준이 성립하지 않는 공간을 다룬다.
• 비유클리드 기하학의 예로서 쌍곡기하학(hyperbolic)과 타원기하학(elliptic geometry)이 있다. 두 기하학은 유클리드 기하학의 제5공준 평행선 공준을 변형한 것이다.
  
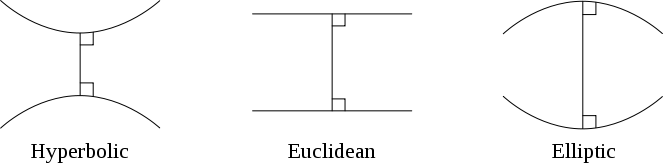
  • 유클리드 기하학에서 ‘한 직선 L 위에 있지 않은 한 점 P가 있을 때 P를 포함하고 L과 만나지 않는 직선이 단 하나 존재한다‘.
  • 쌍곡기하학에서는 ‘한 직선 L 위에 있지 않은 한 점 P가 있을 때 P를 포함하고 L과 만나지 않는 두 직선이 존재한다‘. 안장면 위의 기하학.
  • 타원기하학에서는 ‘한 직선 L 위에 있지 않은 한 점 P가 있을 때 P를 포함하고 L과 만나지 않는 직선이 존재하지 않는다‘. 타원 구 위의 기하학. 지구의 겉면은 타원 기하학을 볼 수 있다.

	유클리드기하학	쌍곡기하학	구면기하학
평행선	단 한개 존재한다.	수없이 많이 존재한다.	존재하지 않는다.
삼각형의 세 내각의 합	180° 삼각형의 넓이에 관계없이 세 내각의 크기의 합은 일정하다.	180°보다 작다. 삼각형의 넓이가 넓어질수록 세 내각의 크기의 합은 작아진다.	180°보다 크다. 삼각형의 넓이가 넓어질수록 세 내각의 크기의 합은 커진다.
측지선(gedesic)	직선 길이는 무한대이다. 두 점을 지나는 직선은 단 한 개 이다.	곡선 길이는 무한대이다. 두 점을 지나는 직선은 한개 이상이다.	대원 길이가 유한이고, 일정하다. 두 점을 지나는 직선은 없다.

 

로바체프스키 기하학의 무모순성

• 로바체프스키 기하학 = 비유클리드 기하학
• 어떤 적당한 기본적인 가정들과 예각의 전제(삼각형의 세 각의 합은 180도보다 작다)를 합친 모임으로부터 전개된 기하학은 유클리드 기하학과 마찬가지로 무모순이다.

리만 비유클리드 기하학

• 일정한 양수 곡률을 가진 곡면
• 둔각의 전제(삼각형의 세 각의 합은 180도를 넘는다)를 만족시킨다.

비유클리드 기하학의 영향

• 평행선 공준을 다른 공준들로부터 유도할 수 없다.
• 서로 모순이 없는 공준들을 선택할 수 있고, ‘인공적인’ 기하학을 창조할 수 있다.(기하학의 해방)
• 기하학의 공준은 ‘자명함’ 또는 ‘진리’와 관계 없다.
• 수학은 인간 정신의 임의의 창조물이다.
• 수학은 가설ㆍ연역적 학문이다.
• 물리적인 공간은 우리의 외적인 경험으로부터 얻은 경험적인 개념이며, 이런 공간을 묘사하기 위해 고안된 기하학의 공준들은 그런 경험의 표현에 불과하다.
• 새롭고 흥미로운 기하학이 대단히 많이 발견되었다.
  • 비아르키메데스 기하학, 비데자르그 기하학, 리만 기하학, 비리만 기하학,?유한 기하학
  • 아인슈타인의 일반 상대성 이론: 리만 비유클리드 기하학의 일반화
  • 시각 공간: 로바체프스키 기하학

28,29)?비가환 대수학의 발견(1843년)

대수적 구조의 발견

• 자연수의 집합 $latex \mathbb{N}$은 이항 연산 ‘덧셈’$latex +$과 ‘곱셈’$latex \times$에 대해 다음 성질을 만족시킨다. $latex a,b\in \mathbb{N}$
  1. $latex a+b = b+a$
  2. $latex a \times b = b\times a$
  3. $latex (a+b)+c = a+(b+c)$
  4. $latex (a \times b) \times c = a \times (b \times c)$
  5. $latex a \times (b+c) = a \times b+a \times c$
• 당시 대수학은 기호화된 산술로 간주됨.
• 자연수 이외의 다른 원소의 집합에도 적용시킬 수 있다.
• 이 모든 체계에 공통된 ‘대수적 구조’, 여기에서는 5가지 기본적인 성질과 이것들의 결과가 존재한다.
• 5가지 성질을 공준으로 간주할 수 있다. 대수학도 가설ㆍ연역적 연구의 주제.

복소수

• 표현: 유향 선분, 평면의 점, 실수의 순서쌍.
• 수 쌍(number couple)의 법칙
  • $latex a=a_1 + a_2 i=(a_1, a_2), b=b_1 + b_2 i = (b_1, b_2)$일 때 다음 법칙이 성립한다.
  • $latex (a_1, a_2)+(b_1, b_2)=(a_1+b_1, a_2+b_2)$
  • $latex (a_1, a_2)\cdot (b_1, b_2)=(a_1 b_1 – a_2 b_2, a_1 b_2 + a_2 b_1)$

비가환 대수학

• 교환 법칙이 성립하지 않는 대수학으로 예를 들어 사원 수와 정사각 행렬이 있다.
• 통상적인 대수학에 대한 공준들을 다양한 방법으로 약화ㆍ삭제하거나 공준의?일부를 다른 공준으로 바꿈으로써 새로운 체계를 만들 수 있다. (연산에 관한 공준으로 산술을 가설ㆍ연역적으로 정리. 대수학이 탄생하고, 공준을 추가ㆍ삭제ㆍ수정하며 새로운 대수학 체계를 만듦. 그 대수학 중 하나가 비가환 대수학.)

사원수 quaternion

• $latex (\mathbb{R},+,\times)$
• $latex (a,b,c,d)=a+bi+cj+dk$
  • $latex i^2=j^2=k^2=-1$
  • $latex ij=k, jk=i, ki=j$
  • $latex ji=-k, kj=-i, ik=-j$
• 순환 순서: i→j→k→i
• 곱셈의 교환법칙이 성립하지 않는다.

30)?군 구조(1830년-1860년)

군(group)

정의(★)

• 집합 $latex G$가 이항 연산 $latex *$에 대해 닫혀 있고, 즉 $latex *:(G,G)\rightarrow G$이고, 다음 세 공준을 만족할 때,?$latex G$를 군(group)이라고 한다.
  • [G1:결합법칙] $latex a,b,c\in G$일 때, $latex (a*b)*c=a*(b*c)$를 만족한다.
  • [G2:항등원 존재] ?모든 $latex a\in G$에 대해 $latex a*i=a$를 만족하는 $latex i\in G$가 존재한다.
  • [G3:역원 존재] 각 $latex a\in G$에 대해?$latex a*a^{-1}=i$를 만족하는?$latex a^{-1}\in G$가 존재한다.
• 만약, [G4:교환법칙] $latex a,b\in G$일 때,?$latex a*b=b*a$ 이면?$latex G$를 가환 군(commutative group) 혹은 아벨 군(Abelian Group)이라고 한다.

대칭 군

• 도형을 변환했을 때 같은 도형이 나오는 변환을 대칭이라고 하자. 그 대칭을 집합?$latex G$가 원소로 가진다. 이때 연산?$latex *$는 대칭을 이어서 하는 순서를 나타낸다.
• 대칭 군의 예
  • 예1: 이등변 삼각형의 대칭 군?$latex G$
    • $latex G={I,r}$, I는 항등 변환, r는 대칭 변환
      
  • 예2: 삼각대의 대칭 군
    • $latex G={I,v,w}$, I는 항등변환, v는 120도 회전, w는 240도 회전.
      
  • 예3: 정삼각형의 대칭 군
    • $latex G={I,v,w}$, I는 항등변환, v는 120도 회전, w는 240도 회전.
      
  • 예5: 정육면체의 대칭 군
    • $latex G$의 원소: 항등 변환,?(면에 관한) 반사 대칭 24개,?(축에 관한) 회전 대칭 24개.
  • 예6: 정12면체의 대칭 군
    • $latex G$의 원소: 항등 변환, (면에 관한) 반사 대칭 60개, (축에 관한) 회전 대칭 60개.

군의 예에서 얻을 수 있는 결론

• 공준 G4(교환 법칙)가 다른 세 개의 공준과 독립적이다.
• 공준 G1, G2, G3, G4는 서로 무모순이다.

군의 중요성

• 많은 대수적 구조는 적당한 이항 연산에 관해 군(또는 반군)을 이룬다. 즉, 하부 구조로서 군 구조를 포함하고 있다.
  
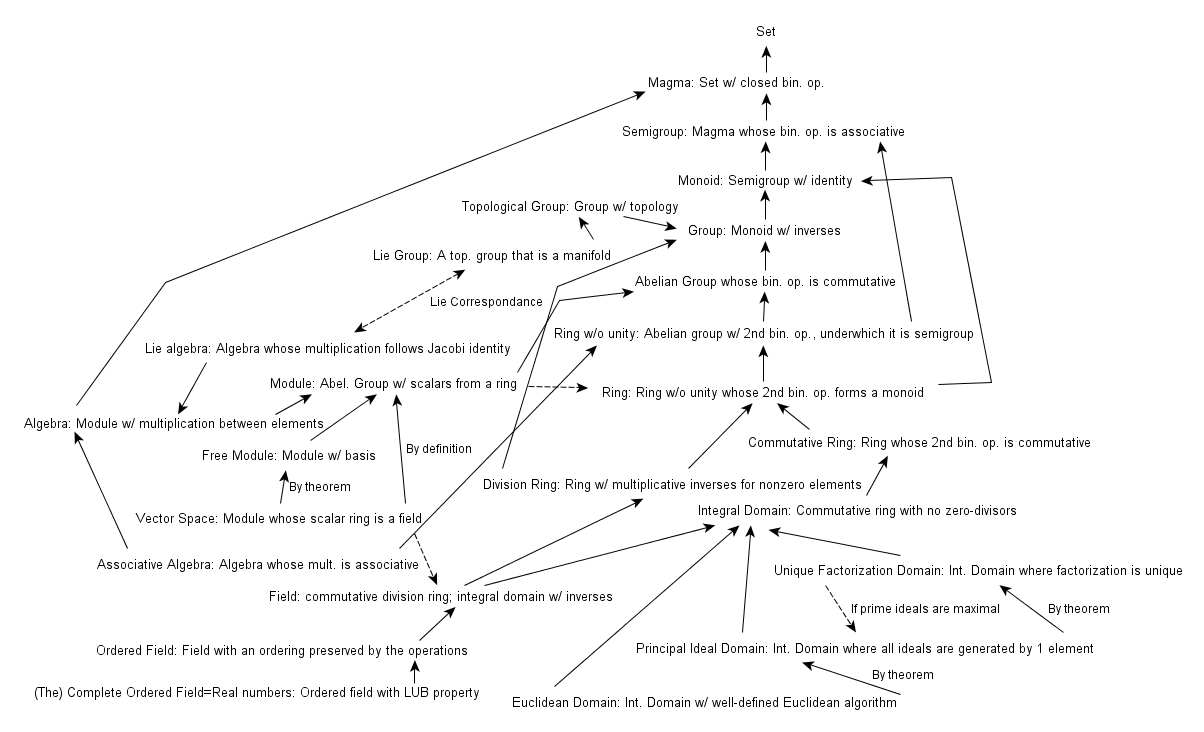
• 군은 많은 대수적 구조를 형성하는 ‘원자’와 같은 역할을 한다.

군과 관련된 다른 개념

• 반군(semigroup)
  • S가 G1만 만족하면 S를 반군이라고 한다.
• 환(ring)
  • S가 군이고,?$latex \times$에 대해 닫혀 있고, 즉 $latex \times :(G,G)\rightarrow G$이고 다음 공준을 만족한다.
    • [결합법칙]$latex a,b,c\in G$일 때, $latex (a\times b)\times c=a\times (b\times c)$를 만족한다.
    • [항등원 존재]모든 $latex a\in G$에 대해 $latex a\times i=a$를 만족하는 $latex i\in G$가 존재한다.
    • [오른쪽 분배법칙] $latex a,b,c\in G$일 때, $latex a\times (b\times c)=(a\times b)+(a\times c)$를 만족한다.
    • [왼쪽 분배법칙] $latex a,b,c\in G$일 때, $latex (b\times c)\times a=(b\times a)+(c\times a)$를 만족한다.
• 가환 환(commutative ring)
  • 환 S에 대해 다음 공준이 성립하면 가환 환이다.
    • [교환법칙]?$latex a,b\in G$일 때, $latex a\times b=b\times a$

31)?에를랑겐 목록(1872년)

에를랑겐 목록(Erlangen Program)

• 1872년에 펠릭스 클라인(Felix Klein, 1849~1925)이 에를랑겐 대학교의 교수로 임용되면서 기하학의 제반 문제들을 해결하기 위해 제안한 연구 방법론이다.
• The Erlangen program is a method of characterizing geometries based on group theory and projective geometry.
• 당시 기하학의 중심은 유클리드 기하학을 모델로 삼아 공리로부터 정리들을 증명해내는 일이었다. 이런 상황에서, 클라인은 두 가지 점에서 혁신적인 제안을 했다.
  • 첫째, 그는 대칭의 개념을 담고 있는 대수적인 이론인 군론이야말로 기하학적 지식을 종합해 낼 올바른 토대라고 주장했다.
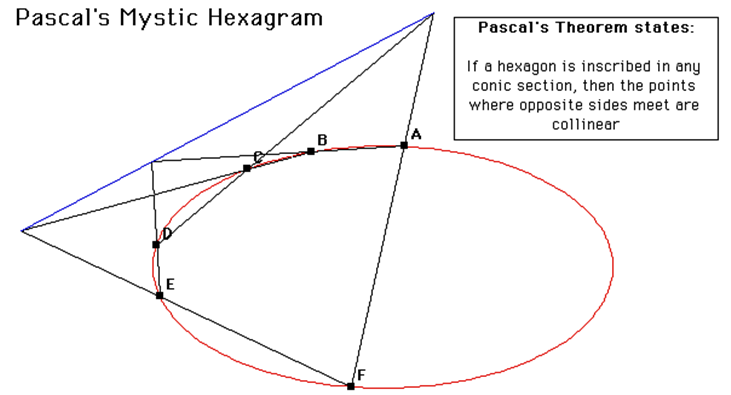
  • 둘째, 그는 각 기하학적 언어에 대해 그에 맞는 개념들이 있다고 주장했다.예를 들어, 사영기하학은 원뿔곡선을 다루기에는 적합하지만 사영변환에 대해 불변이 아닌 원이나 각도 개념은 제대로 다룰 수 없다는 것이다. 이와 같이 기하학은 여러 언어를 필요로 하며, 이 각각의 언어들을 대칭군으로 설명할 수 있다는 것이 클라인의 제안이었다.
• 그 결과,
  • 군 론을 이용해 기하학을?체계적으로 설명함. 모든 기하학을 체계적으로 분류하는 깔끔한 방법을 제공함.
  • 기하학을 정의할 수 있게 되었다.
  • 당시의 모든 기하학을 요약, 기하학에서 새롭고 풍요로운 연구 방향 제시했다.
• 변환 군의 포함 관계
  • 계량적인 유클리드 ? 닮음 ? 중심아핀 ? 아핀 ? 사영 [? 위상]

32)?해석학의 산술화: 수학의 기초로서의 자연수 체계(19세기 말)

미분 적분학의 간략한 역사

• 적분법은 넓이, 부피, 호의 길이 등을 찾는 문제를 연구하면서 탄생했다.
• 미분법은 곡선에 접선을 그리는 문제, 함수의 최댓값최솟값을 찾는 문제를 연구하면서 탄생했다.

미분적분학의 기본 정리

• 정리1. 미분과 적분의 관계
  \frac{d}{dx}\int_{a}^{x}f(t)dt=f(x)
• 정리2. 정적분의 기본정리
  \int_{a}^{b}f(t)dt=F(b)-F(a),F'(x)=f(x)
• 대수적인 접근으로 적분을 형식적으로 수행할 수 있는 도구로서 미분 적분학의 기본 정리를 활용했다. 연산으로서 미분법과 적분법이 탄생한 배경이다.

수학의 분류

• 기하학, 대수학, 해석학
• 해석학에서 극한 개념은 중요한 역할을 하므로, 일반적으로 극한 개념의 존재가 대수학으로부터 해석학을 구별 짓는다.

미분 적분학의 불완전한 기초에 대한 비판

• 뉴턴의 유율법은 o를 도입할 때?없어지지 않는 것으로 가정한 반면에 마지막에서?그 값을 0으로 택한다. 그렇다면?o은 0인가, 0이 아닌가. 라이프니츠이 미분법도 이 논리적 결함을 가지고 있었다.
• 이 미분법은 미분 결과를 계산하는 경우가 대부분이라 결함을 해결하려는데 관심을 두지 않았다.
• 물리적인 문제에 그 결론을 적용해서 얻은?성공은 그 수학 자체가 틀림없이 정확하다는 확신을 주었다.
• 급수의 합은 수렴하는 급수에 대해서만 논해야 하지만, 발산하는 급수를 수렴하는 급수처럼 다루어 많은 오류를 낳았다.

해석학의 엄밀화 계획

• 극한 개념을 부등식에 기초해서 번역하고 증명한다.
• 극한 이론을 전개하고 극한 개념을 이용해서 연속성, 미분법, 정적분법 등을 정의했다.
• 코시는 극한, 무한소, 연속에 관해 정의했다. 그 정의들은 근본적으로 옳았지만 사용된 말은 모호하고 불명료했다. 그 정의들은 연속 운동의 개념을 이용했다. 예를 들어 ‘고정된 값에 한없이 접근한다’, ‘한없이 작아진다’와 같은 표현을 썼다.
• 리만(Bernhard Riemann, 1826~1866)와 바이어슈트라스(Karl Weierstrass, 1815~1897) 등은 이때까지 정의했던 극한, 무한소, 연속에 대한 정리에 대한 반례를 구성해 해석학이 엄밀해져야 함을 주장해다.

해석학의 산술화

• 극한 개념에 대한 명확한 ‘대수적(혹은 산술적)’ 정의를 제공해서 코시의 직관적이고 ‘운동학적인’ 개념을 대체해야 했다.
• 해석학의 산술화 1단계
  • 실수 체계에 대한 공준 집합 설정 → 실수를 완비 순서체로 공리화?→ 해석학은 무모순
• 실수를 완비 순서체로 공리화
  • 실수는 다음 세 공리를 만족하는 집합이라고 한다.
  • 1. 체 공리
  • 2. 순서 공리
  • 3. 완비성 공리
    • R의 비지 않은 부분 집합 S가 위로 유계이면 S의 (실수이고 유일한) 최소 상계가 존재한다.
• 해석학의 산술화 2단계
  • 입실론-델타 과정을 도입해서 현재 해석학에서 쓰이고 있다.
  • ‘수열의 극한‘의 정의
    • For each real number ε > 0, there exists a natural number N such that, for every natural number n>N, we have |x(n)-x|<ε.
    • Then, x is the limit of the sequence x(n).
  • ‘함수의 극한‘의 정의
    • For every real ε > 0, there exists a real δ > 0 such that for all real x, 0 < | x ? p | < δ implies | f(x) ? L | < ε.
    • Then, L is the limit of the function f(x) at x=p.

33)?수학의 기초로서의 집합론(19세기 말)

• set theory = 집합론 = 모음 이론
• 현대 수학의 기초는 집합론이다.

시대에 따른 수학의 기초

• 고대 그리스: 기하학
• 중세, 르네상스 시대: 기하학
• 17세기, 18세기의 미분적분학 시대: 대수학 (코시의 연구에는 대수적인 면과 기하적인 면이 혼재한다.)
• 19세기 후반기: 산술
• 1880년대 이후: 집합론

집합론의 중요성

대단히 많은 수학의 무모순성이 자연수 체계의 무모순성에 의존한다. 그런데?자연수 체계를 집합론에서 출발해서 얻을 수 있다. 그러므로 집합론이 무모순이면 자연수 체계는 무모순이고, 따라서 많은 수학이 무모순이다.

집합론에서 중요한 개념

• 일대일 대응
• 동치
  • 집합 A와 집합 B가 동치이다. = A에서 B 혹은 B에서 A로 일대일 대응 함수가 존재한다.
• 기수
• 유한 집합과 무한 집합

연습 문제

• 동치인 두 집합의 기수는 같다. 기수에 대해 |A|+|B|=|A∪B|가 성립한다. ?이때, 이항 연산 +를 덧셈이라고 부른다. 기수의 덧셈이 교환적이고 결합적임을 보여라.
  • 기수의 덧셈의 정의에 따라 |A∪B|=|A|+|B|이고 |B∪A|=|B|+|A|이다.
  • 집합론에 따라 A∪B=B∪A이므로 |A∪B|=|B∪A|이다.
  • 따라서, 기수의 덧셈은 교환법칙|A|+|B|=|B|+|A|이 성립한다..
  • 또, 집합론에 따라 A∪(B∪C)=(A∪B)∪C이고,
  • |A∪(B∪C)|=|A|+|(B∪C)|=|A|+(|B|+|C|)와
  • |(A∪B)∪C|=|(A∪B)|+|C|=(|A|+|B|)+|C|가 성립한다.
  • 따라서, 기수의 덧셈은 결합법칙 |A|+(|B|+|C|)=(|A|+|B|)+|C|이 성립한다.
  • (A와 B가 유한 집합이면 자연수의 덧셈을 정의할 수 있다.)
• 기수에 대해 |A||B|=|A×B|가 성립한다.?기수의 곱셈은 교환적, 결합적이고, 기수의 덧셈에 관해 배분적임을 보여라.
  • |A×B|=|A||B|이고?|B×A|=|B||A|이므로 기수에 대한 교환법칙이 성립한다.
  • |A×(B×C)|=|A||B×C|=|A|(|B||C|)이고?|(A×B)×C| = |A×B||C| = (|A||B|)|C|이다.
  • 집합론에 따라 A×(B×C) = (A×B)×C이므로 |A|(|B||C|) = (|A||B|)|C| 이므로 기수의 곱셈은 결합법칙이 성립한다.
  • B∪C=Ø 라 하자.
  • |A×(B∪C)| = |A||B∪C| = |A|(|B|+|C|)이고
  • |(A×B)∪(A×C)| = |A×B|+|A×C| = |A||B|+|A||C|이다.
  • 집합론에 따라?A×(B∪C) = (A×B)∪(A×C)이므로 기수의 곱셈은 기수의 덧셈에 대해 분배법칙 |A|(|B|+|C|) = |A||B|+|A||C| 이 성립한다.

이과 같이 집합론으로부터 상당한 정도로 수학이 일반화 되었다.

집합론에 의한 일반화 사례

• 기하학의 도형은 점의 집합[모음]으로 나타내었다.
• 함수를 두 집합의 관계[곱집합]로 나타내었다.
  • X에서 Y로의 함수 f (a function f from X into Y)
    • $latex f:X\rightarrow Y$
    • $latex f=\{(x,y)\in X\times Y \ | \ \forall x\in X \Rightarrow \exists !(x,y)\}$
  • X에서 Y위로의 함수 f (a function f from X?onto Y)
    • $latex \{f(x)\}=Y$
  • 일대일 함수 f
    • For every $latex x_1,x_2\in X$, $latex x_1\neq x_2 \Rightarrow f(x_1)\neq f(x_2)$.

34) 무한 모음과 초한수(1874년-1895년)

• ?무한 집합이 그것의 진부분집합과 일대일 대응이 될 수 있다는 것을 발견.
  • 예를 들어, $latex \mathbb{N}\supset \{n\in \mathbb{N}\ |\ n\geq2\}$이고 일대일대응 함수 $latex f(n)=n+1$가 존재하므로 \mathbb{N}는 무한 집합이다.
• 무한 집합의 정의(데데킨트의 정의)
  • M이 자신의 진부분집합과 동치이면 M은 무한 집합이다. 동치가 아니면 M은 유한 집합이다.
• 일대일대응 함수 $latex f(n)=n^2$가 존재하므로 $latex \mathbb{N}\sim \mathbb{N}^2$이다.
• 동치인 모음들의 기수는 서로 같다.
• 유한 모음의 기수는 자연수이며, 무한 모음의 기수는 초한수(transfinite number)이다.
• 셀 수 있는 모음(countable set)
  • $latex |\mathbb{N}|=|\mathbb{Z}|=|\mathbb{Q}|=\aleph_0$
• 셀 수 없는 모음(uncountable set)
  • $latex |\mathbb{R}|=|[0,1]|=\aleph_1=c$
• 초월수(transcendental number)
  • 정수 계수로만 이뤄진 유한 차수 다항식의 해가 될 수 없는 수들을 초월수라고 한다.
• 대수적인 수(algebraic number)
  • 수 계수로만 이뤄진 유한 차수 다항식의 해가 될 수 있는 수들을 대수적인 수라고 한다.
• 연속체 가설(continuum hypothesis)
  • $latex \aleph_0$보다 크고 $latex c$보다 작은 기수는 존재하지 않는다. 즉,?$latex \aleph_1 =c$
  • 두 명제 $latex \aleph_1 =c$와 $latex \aleph_1 \neq c$는 집합론의 공준 집합으로 증명할 수 없다는 사실이 증명되었다.
  • 연속체 가설은 체르멜로ㆍ프렌켈 공준 집합과 독립적이다.
  • 체르멜로ㆍ프렌켈 공준 집합은 집합론의 공준 집합이다.
  • 현재 집합론에서 연속체 가설을 참으로 가정하고 이용해도 된다.

35)?형식적 공리학(20세기 초)

힐베르트의 ≪기하학의 기초≫

• 유클리드 평면 기하학과 공간 기하학을 무정의 용어 6개와 공리 20(or 21)개
  에 근거해서 전개
  • 무정의 용어: 점, 선, 면
  • 무정의 관계: ‘~에 놓여 있는’, ‘결합(incidence)’, ‘~사이에 있는(between)’, ‘순서(order)’, ‘합동(congruence)’
  • 공리:?결합 8개, 순서 4개, 합동 5개, 평행 1개, 연속 2개

공리적 방법의 재등장

• 비유클리드 기하학과 비가환 대수학의 발견, 해석학의 산술화에 대한 오랜 탐구 등은 공리화 과정을 더 깊이 연구하게 만들었다.
• 공리적 방법에 대한 이런 개선 작업에 가장 큰 영향을 끼친 것은 힐베르트의?≪기하학의 기초≫였다.
• 대수학에서?군, 환, 체, 벡터 공간 – 19세기 말
• 해석학에서?해석학의 산술화 → 실수의 산술화?→ 자연수(즉, 산술)의 기초에 대한 문제
• 자연수의 공리 체계- 19세기 말, 데데킨트, 페아노, 프레게의 연구

형식적 공리학

• 명제 함수
  • ‘봄은 계절이다’의 명제 함수 P(x,y)=’x는 계절이다’.
• 형식적 공리학의 양식
  • 1. 논술의 ‘기본적인 용어’ – 무정의 용어
  • 2. 논술의 ‘공준’ 또는 ‘공리’ P (1과 2 부분을 통틀어 논설의 ‘기초’)
  • 3. 용어는 이미 도입된 용어로 정의
  • 4. 논술의 ‘정리’ T
  • 5. 공준 P는 정리 T를 함의한다.
• ‘기본적인 용어’는 변수로 나타낼 수 있다.
• 공준 P는 기본적인 용어에 관한 문장이며 명제 함수이다.
• 정리 T는 공준 P에 의해 함의되므로 T는 명제 함수이다.

36)?수학의 정의(20세기 초)

형식적 공리학에서 정의와 그에 따른 공준으로부터 여러 정리를 유도해본다.

예로서 이가 관계(dyadic relation)를 정의한다. 집합 $latex K={a,b,c,d}$일 때, K의 임의의 원소 a,b에 대해 ‘a가 b와 R-관계가 있다’는 것은 $latex aRb$로 나타내고 $latex a=b$이면 a와 b는 서로 같은 원소이다.

이 정의로부터 공준 4개를 얻을 수 있고, 이 공준들로부터 다양한 정리를 유도할 수 있다.

집합 S={사람 A, A의 아버지, A의 할아버지, A의 증조 할아버지}에서 관계 $latex aRb$을 ‘a는 B의 조상이다’라고 하자. 그러면 이가 관계로부터 얻은 정리들은 S에 대해 모두 성립한다. ? S를 대상으로 그 정리들은 모두 증명할 필요가 없다. 이것이 공리적 방법의 강점이다. 따라서 이런 공리적 방법이 ‘경제적’임을 알 수 있다.

37) 초수학(1899년~1920년)

공준 체계의 성질

• 동치성(equivalence)
  • 두 공준 체계에 대해 한 체계의 기본적인 용어들을 다른 체계의 기본적인 용어들로 정의할 수 있고 한 체계의 공준들을 다른 체계의 공준들로부터 유도할?수 있을 때, 두 체계는 ‘동치’라고 한다.
• 무모순성(consistency)
  • 명제 $latex p$와 그 부정 $latex ~p$가 함께 참이 되지?않는 공준 집합을 ‘무모순’이라 한다.
• 독립성(independence)
  • 무모순인 공준 집합의 한 공준이 그 집합의 다른 공준들로부터 논리적으로 유도되지 않을 때, 그 공준은 ‘독립적’이라 한다.
• 완전성(completeness)
  • 무모순인 공준 집합에 대해, 기본적인 용어를 확장하지 않고 주어진 공준들과?독립적이고 무모순인 또 다른 공준을 그 공준 집합에 추가할 수 없을 때, 그?공준 집합은 ‘완전’하다고 한다.
• 절대성(categoricalness)
  • 공준 집합에 대한 임의의 두 해석이 서로 동형일 때, 그 공준 집합은 ‘절대적’이라 한다.

수학의 기초에서 제3의 위기

수학의 기초는 기하학, 대수학, 산술을 거쳐 모음 이론이 담당하게 되었다. 그런데 이 모음 이론의 공준에서 모순이 발견된다.

칸토어의 역설

• $latex U$가?모음 전체의 모음이라 하자. 그러면 일반적인 모음의 성질에 따라 $latex card(P(U))>card(U)$이다. 그러나 $latex U$의 정의에 따라 $latex U$는 모든 모음을 포함하므로 $latex P(U)\subset U$이고 따라서 $latex card(P(U))\le card(U)$이다. 마지막 결론은 역설[모순]을 일으킨다.

러셀의 역설

• $latex C=\{A|A\notin A\}$ 가 있다. $latex C\in C$이면 $latex C\notin C$라는 모순이 생긴다. 반대로,?$latex C\notin C$이면?$latex C\in C$라는 모순이 생긴다. 이 역설을 ‘러셀의 역설’이라고 한다.

고틀로프 프레게(Gottlob Frege, 1848~1925)는 산술을 기초를 모음 이론으로 삼는 이론을 발전시켰는데 모음 이론의 모순을 발견하고 비통해 했다.

다양한 사람들이 모음 이론의 모순을 해결하기 위해 노력했다. 단순히 모순을 제거하거나 비술어적 정의(정의하는 용어를 이용해 정의)를 제한하는 시도를 했다. 이 모순을 해결하기 위해 논리주의, 직관주의, 형식주의 학파가 등장했다.

38) 괴델의 불완전성 정리(1931년)

집합론[모음 이론]의 역설로부터 수학의 흔들리는 기초를 확실한 토대 위해 세우기 위해 나타난 수리 철학 학파

• 논리주의(러셀, 프레게)
• 직관주의(브로우베르)
• 형식주의(힐베르트)

논리주의

• ‘수학이 궁극적으로 논리학으로만 유도될 수 있다’는 생각.
• 논리적 개념 이외의 개념에 수학적 실체를 부여하지 않았다.
• 논리주의를 주장한 대표적인 수학자: 조지 불(George Bool, 1815~1869),?오거스터스 드모르간(Augustus De Morgan, 1806~1871),?주제페 페아노(Giuseppe Peano, 1858~1932),?알프레드 화이트헤드(Alfred North Whitehead, 1861~1947),?버트런드 러셀(Bertrand Russell, 1872~1970)

직관주의

• ‘수학은 반드시 유한한 구성적인 방법에 의해, 직관적으로 주어진 자연수 위에 건설되어야 한다’는 생각.
• 배중율은 유한 모음에서만 합법적이다.
• 직관주의를 주장한 대표적인 수학자: 라위천 브로우베르(Luitzen?Brouwer, 1882~1966),?크로네커,?헤르만 바일(Hermann Weyl)

형식주의

• 수학은 형식적인 기호 체계에 관한 학문이다. 수학은 추상적인 전개의 모임이다. 추상적인 전개에서 용어는 단순히 기호이며 명제는 이 기호들을 포함한?공식이다. 수학의 궁극적인 기저는 논리학에 놓여있지 않고, 논리 이전의 표시?또는 기호의 모임과 이런 기호들의 연산의 집합에 놓여있다.
• 수학은 구체적인 내용을 포함하지 않고 단지 관념적인 기호 원소만을 포함하기 때문에, 수학의 여러 분야에 대한 무모순성의 확립은 형식주의 학파의 계획에서 중요하고 필수적인 부분이 된다.

괴델의 불완전성 정리(G?del’s Incompleteness Theorems)

첫째 정리

자연수 체계를 포함하는 무모순인 형식적인 체계 $latex F$가 존재하면,?$latex F$안에 증명할 수 없는 명제$latex S$가 존재한다.

• 골드바흐의 추측(Goldbach’s conjecture – “4 이상의 모든 짝수는 두 소수의 합으로 나타낼 수 있다.”)가 앞서 말한 ‘증명할 수 없는 명제$latex S$’일 수 있다.

둘째 정리

자연수 체계를 포함하는 무모순인 형식적인 체계 $latex F$가 존재하면, $latex F$의 무모순성을 $latex F$안에 존재하는 명제만으로 증명할 수 없다.

괴델의 불완전성 정리의 의미

• 수학에 모순이 없다고 보장할 수 없다. =?수학의 확실성을 보장할 수 없다.
• 수학적으로는 모든 문제를 풀어내는 일반적이고 기계적인 절차란 있을 수 없다.
  • 수학의 모든 문제를 컴퓨터로 해결할 수 없다.
• 수학은 완전한 학문이 될 수 없다.
  • 수학에서 모든 중요한 분야를 완전히 공리화할 수 없다.

39) 셈틀[현대의 전자 계산기](1944년)

셈틀[계산기] 발명의 역사

• 1642년 파스칼의 덧셈 기계
• 17세기 말 라이프니츠의 곱셈 시계
• 찰스 배비지(Charles Babbage)의 차분 기관. 6자리 수를 계산 가능.
• 배비지의 해석 기관. 50자리수를 1000개 저장 가능.
• 폰 노이만(von Neumann)의 EDVAC
• IBM PC, Apple Computer

셈틀과 수학

• 수론에서 가장 큰 씨수[소수]를 찾거나 골드바흐의 추측을 만족시키는 가장 큰 수를 찾는데 셈틀을 사용한다.
• 미분 방정식의 해를 수치적으로 셈틀을 이용해 구한다.
• 초월수의 근사값을 구하는데 셈틀을 이용한다.
• 새로운 수학분야, 예를 들어 알고리즘 분석, 최적환 이론 등을 발전시켰다.
• 조합론과 그래프 이론 등 오래 전에 연구된 분야가 다시 활발하게 연구되기 시작했다.
• 네 색 문제(four colors problem)을 해결하는데 셈틀이 쓰였다.
• 사람이 증명이 긴 정리는 다른 사람이 그것을 따라가며 검증을 했다고 하더라도 사람이기 때문에 검증에 실수가 있는 경우를 배제할 수 없다. 긴 증명은 사람이 검증했더라도 신뢰도가 떨어진다. 인간이 검증한 증명도 100%확률론 정확하다고 볼 수 없다. 따라서 확률론적인 증명도 신뢰할 만하다. 확률론적인 증명은 예를 들어 99.9%의 높은 확률로 참인 명제의 증명을 말한다.
• 마방진에 관한 증명 과정은 단순한 계산이 반복적으로 요구된다. 이때, 사람이 증명하기보다 셈틀에 의존해 증명하는 것이 더 정확하다. 셈틀에 의한 증명이 필요할 때가 있다.

수리 철학자들의 최근 생각

• 수학은 완벽하지 않으며 인간적이다.
• 수학적 지식은 오류에 빠질 수 있다.
• 경험적 증거, 수치적 실험, 확률론적 증명은 모두 우리가 수학에서 믿어야 할 것을 결정하는데 도움을 준다.